Gold Isn't General: Why Olympiad Wins Don't Signal AGI—and What Schools Should Do Now

AI’s IMO gold isn’t AGI

Deploy it as an instrumented calculator

Require refusal metrics and proof logs

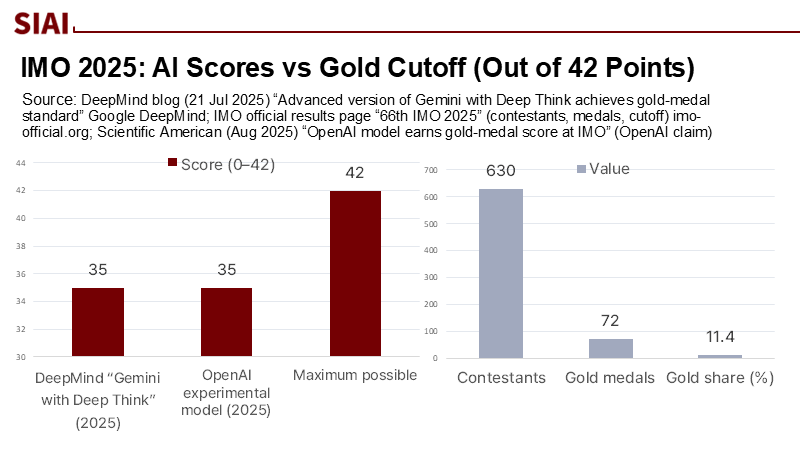
In July 2025, two advanced AI systems achieved "gold medal–level" results in the International Mathematical Olympiad (IMO), solving five out of six problems in the 4.5-hour timeframe. Verified by Google DeepMind, these results were matched by OpenAI's experimental model. Despite this, over two dozen human participants still outperformed the machines, with about 11% of the 630 students earning gold medals. This achievement is noteworthy, as DeepMind's systems had only reached silver the previous summer. The significance lies not in reaching artificial general intelligence but in combining effective problem-solving with a safety mechanism known as strategic silence, which raises essential considerations for educational institutions regarding AI implementation and regulation.

Reframing the Achievement: From General Intelligence to Domain-Bounded Mastery

The prevailing narrative treats an Olympiad gold as a harbinger of generalized reasoning. A more defensible reading is narrower: these systems excel when the task can be formalized into stepwise deductions, search over structured moves is abundant, and correctness admits an unambiguous verdict. That is precisely what high-end competition math provides. DeepMind's 2024 silver standard required specialized geometry engines and formal checkers. By 2025, both labs will combine broader language-based reasoning with targeted modules and evaluation regimes to reach gold on unseen problems. This is impressive engineering, but it does not necessarily demonstrate that the same models can resolve ambiguous, real-world questions where ground truth is contested, noisy, or deferred. In classrooms, this distinction is particularly relevant now because education systems are under pressure—following record declines on PISA mathematics and uneven NAEP recovery—to bridge capability gaps with the help of AI. If we mistake domain-bounded mastery for general intelligence, we risk deploying tools as oracles where they should be framed, regulated, and assessed as instrumented calculators.

The New Safety Feature: Strategic Silence Beats Confident Error

A lesser-discussed aspect of the IMO story is abstention. Where earlier systems "hallucinated," newer ones increasingly decline to answer when internal signals flag inconsistency. In math, abstention is straightforward to reward: either a proof checks or it does not, and a blank is better than a confidently wrong derivation. Recent research formalizes this with conformal abstention, which bounds error rates by calibrating the model's self-consistency across multiple sampled solutions. A 2025 work shows that learned abstention policies can further improve the detection of risky generations. The upshot is that selective refusal, rather than omniscience, underpinned part of the Olympic-level performance. Transfer that tactic to messy domains—such as ethics, history, and policy—and the ground shifts: the equivalence between answers is contestable, and calibration datasets are fragile. Education policy should therefore require vendors to publish refusal metrics alongside accuracy—how often and where the system declines—and to expose abstention thresholds so that schools can adjust conservatism in high-risk contexts. That is how we translate benchmark discipline into classroom safety.

Proof at Scale—But Proof of What?

A parallel revolution makes Olympiad success possible: large, synthetic corpora of formal proofs in Lean, improved autoformalization pipelines, and verifier-in-the-loop training. Projects like DeepSeek-Prover and subsequent V2 work demonstrate that models can produce machine-checkable proofs for competition-level statements; 2025 surveys chart rapid gains across autoformalization workflows, while new benchmarks audit conversion from informal text to formal theorems. This scaffolding reduces hallucination in mathematics because every candidate proof is mechanically checked. Yet it does not imply discovery beyond the frontier. When ground truth is unknown—or when a novel conjecture's status is undecidable by current libraries—models can only resemble discovery by recombining lemmas they have seen. Schools and ministries should celebrate the verified-proof pipeline for what it offers learners: transparent exemplars of sound reasoning and instant feedback on logical validity. But they should resist the leap from 'model can prove' (i.e., demonstrate the validity of a statement based on existing knowledge) to 'model can invent' (i.e., create new knowledge or solutions), especially in domains where no formal oracle exists. Policy should encourage the use of external proof-logs and independent reproduction whenever AI-generated mathematics claims novelty.

Education's Immediate Context: A Capability Spike Amid a Learning Slump

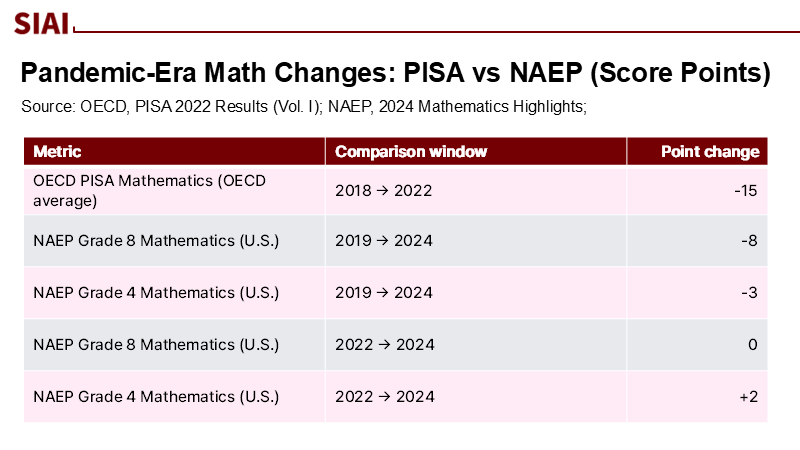
The timing of math-capable AI collides with sobering data. Across the OECD, PISA 2022 recorded the steepest decline in mathematics performance in the assessment's history—approximately 15 points on average compared to 2018, equivalent to about three-quarters of a year of learning—while a quarter of 15-year-olds are low performers across core domains. In the United States, the 2024 NAEP results indicate that fourth-grade math scores are increasing from 2022 but remain below those of 2019, and eighth-grade scores are stable after a record decline. Meanwhile, teacher shortages have intensified: principals reporting shortages rose from 29% to nearly 47% between 2015 and 2022, and global estimates warn of a 44-million teacher shortfall by 2030. In short, demand for high-quality mathematical guidance is surging, while supply lags. The risk is techno-solutionism—handing a brittle tool too much agency. The opportunity is targeted augmentation: offload repetitive proof-checking and step-by-step hints to verifiable systems while elevating teachers to orchestrate strategy, interpretation, and meta-cognitive instruction that machines still miss.

A Data-First Method for Sensible Deployment

Where complex numbers are missing, we can still build transparent estimates to guide practice. Consider a district with 10,000 secondary students and a mathematics teacher vacancy rate of 8%. If a verified-proof tutor reduces the time teachers spend grading problem sets by 25%—a conservative assumption derived from automating correctness checks—. Each teacher reclaims 2.5 hours weekly for targeted small-group instruction, total high-touch time rises by roughly 200 teacher-hours per week (10,000 students / ~25 per class, ≈ 400 classes; 8% vacancy implies 32 classes unstaffed; reclaimed time across 368 staffed classes yields ≈ 920 hours; assume only 22% of those hours translate to direct student time after prep/admin leakage). Under these assumptions, the average small-group time per student could increase by 12–15 minutes weekly without changing staffing levels. The methodology is deliberately conservative: we heavily discount reclaimed hours, assume no gains from lesson planning, and ignore positive spillovers from improved diagnostic data. Pilots should publish these accounting models, report realized efficiencies, and include a matched control school to prevent Hawthorne effects from inflating early results. The point is not precision; it is falsifiability and local calibration. The responsible deployment of AI is crucial for the future of education, underscoring the weight of decisions that policymakers must make.

Guardrails That Translate Benchmark Discipline into Classroom Trust

Policy should codify the differences between math-grade reliability and real-world ambiguity. First, treat math-competent AI as an instrumented calculator, not an oracle: require visible proof traces, line-by-line verifier checks when available, and automatic flagging when the system shifts from formal to heuristic reasoning. Second, adopt abstention-first defaults in high-stakes settings: if confidence falls below a calibrated threshold, the system must refuse, log a rationale, and route to a human. Third, mandate vendor disclosures that include not only accuracy but also a refusal profile—the distribution of abstentions by topic and difficulty—so schools can align system behavior with their risk tolerance. Fourth, anchor adoption in international guidance: UNESCO's 2023–2025 recommendations emphasize the human-centered, transparent use, teacher capacity building, and local data governance; OECD policy reviews highlight severe teacher shortages and the need to support staff with accountable technology, rather than inscrutable systems. Finally, ensure every procurement bundle includes professional learning that teaches educators to audit the machine, not merely operate it.

Anticipating the Critiques—and Meeting Them With Evidence

One critique claims that a gold-level run on Olympiad problems implies imminent generality: if models solve novel, ungooglable puzzles, why not policy analysis or forecasting? The rebuttal is structural. Olympiad items are adversarially designed but exist in a closed world with crisp adjudication; success there proves competence at formal search and verification, not cross-domain understanding. News reports themselves note that the systems still missed one of six problems and that many human contestants scored higher—a sign that tacit heuristics and creative leaps still matter. A second critique warns that abstention may mask ignorance: by refusing selectively, models could avoid disconfirming examples. That is why conformal-prediction guarantees are valuable; they bound error rates on calibrated distributions and make abstention auditable rather than cosmetic. A third critique says: even if not general, shouldn't we deploy aggressively given student losses? Yes—but with verifiers in the loop, refusal metrics in the contract, and open logs for academic scrutiny. The standard for classroom trust must exceed the standard for leaderboard wins.

The Real Payoff: Moving Beyond Answers to Reasoning

If gold is not general, what is the benefit of today's models? In education, it is the chance to make reasoning—the normally invisible scaffolding of problem-solving—observable and coachable at scale. With formal tools, students can identify where a proof fails, edit the line, and instantly see whether a checker confirms or rejects the fix. Teachers, facing overloaded rosters, can reallocate time from marking to mentoring. Policymakers can define success not as "AI correctness" but as student transfer: the ability to recognize invariants, choose lemmas wisely, and explain why a tactic applies. This reframing turns elite-benchmark breakthroughs into pragmatic classroom levers. It also acknowledges limits: outside math, where correctness admits no oracle, explanation will be probabilistic and contestable. Hence, the need arises for abstention-aware systems, domain-specific verifiers where they exist, and professional development that equips teachers with the language of uncertainty. Progress on autoformalization and prover-in-the-loop pipelines is the technical foundation; human judgment remains the ultimate authority.

Back to the statistic, forward to action

A year ago, the top AI could only achieve a silver standard at the IMO; this summer, two laboratories surpassed the gold standard, while many young competitors still surpassed them. This statistic is illuminating not because it predicts AGI, but because it shows the nature of genuine advancement: narrow fields with dependable verification are yielding to systematic exploration and principled restraint. Educational institutions should react similarly. View math-capable AI as an enhanced calculator with logs, rather than as an oracle; require metrics on refusals and proof traces; enhance teacher capabilities so that recovered time can be transformed into focused feedback; and demand independent verification for any claims of innovation. By aligning procurement, teaching methods, and policy with this understanding, Olympiad gold will benefit students rather than lead us into overstatements. The immediate goal is not general intelligence; it is broad reasoning literacy across a system that is still healing from significant educational setbacks. That is the achievement worth pursuing.

The views expressed in this article are those of the author(s) and do not necessarily reflect the official position of the Swiss Institute of Artificial Intelligence (SIAI) or its affiliates.

References

Ars Technica. (2025, July). OpenAI jumpthe s gun on International Math Olympiad gold medal announcement.

Axios. (2025, July). OpenAI and Google DeepMind race for math gold.

CBS News. (2025, July). Humans triumph over AI at annual math Olympiad, but the machines are catching up.

DeepMind. (2024, July). AI achieves silver-medal standard solving International Mathematical Olympiad problems.

DeepMind. (2025, July). Advanced version of Gemini with Deep Think officially achieves gold-medal standard at the International Mathematical Olympiad.

National Assessment of Educational Progress (NAEP). (2024). Mathematics Assessment Highlights—Grade 4 and 8, 2024.

OECD. (2023). PISA 2022 Results (Volume I): The State of Learning and Equity in Education.

OECD. (2024). Education Policy Outlook 2024.

UNESCO. (2023; updated 2025). Guidance for generative AI in education and research.

Xin, H., et al. (2024). DeepSeek-Prover: Advancing Theorem Proving in LLMs (arXiv:2405.14333).

Yadkori, Y. A., et al. (2024). Mitigating LLM Hallucinations via Conformal Abstention (arXiv:2405.01563).

Zheng, S., Tayebati, S., et al. (2025). Learning Conformal Abstention Policies for Adaptive Risk (arXiv:2502.06884).